Baryonification
Publications | | Links: BaryonForge
Having spent the last five years comparing simulations through a variety of their halo properties (see Baryon Imprints) I have used my recent time building phenomological models. When performing cosmological analyses, a standard approach is to marginalize over astrophysical nuisances in the typical sense,
\(P({\rm cosmo}) \propto \int P({\rm cosmo} \mid {\rm astro pars.})\, P({\rm astro pars.})\).
This can be done by varying a set of hyper parameters of the astrophysical model. However, in reality, the required operation is
\(P({\rm cosmo}) \propto \int P({\rm cosmo} \mid {\rm astro pars.}, {\rm astro models.})\, P({\rm astro pars.} \mid {\rm astro models.}) \, P({\rm astro models.})\).
That is, it is not adequate to just marginalize over the astrophysics parameters but we need to marginalize over the space of models as well. The latter is an ill-defined question and cannot be answered in a principle manner. Many different experts have come up with different (equally reasonable) astrophysical models that solve different sets of equations for the macrophysic approximation to astrophysical processes.
Baryonification is an approach that circumvents this issue for the density field, by connecting the baryon signatures in the density field directly to observables — such as halo profiles and gas/star fractions — rather than microphysical equations from different astrophysics processes. Thus, observables can be constrained with available datasets and the model can be used to generate predictions for the density field signatures.
Map-level Baryonification
In Anbajagane, Pandey & Chang 2024 we introduced a coherent, robust model for implementing Baryonification at the map-level. The original technique is used on particle snapshots from an N-body simulation. Particles are radially offset from their nearest halo in a manner that mimics the impact of baryons. However, this process is expensive in both computing and storage requirements. In BaryonForge we introduce a method that works directly at the map-level, incorporating the projection effects and pixel convolutions. This method has since been validated in Zhou, Gatti, Anbajagane, Dodelson+ 2025 and found to model the lensing field at \(1\%\) simultaneously for a variety of higher-order statistic and redshift bins.
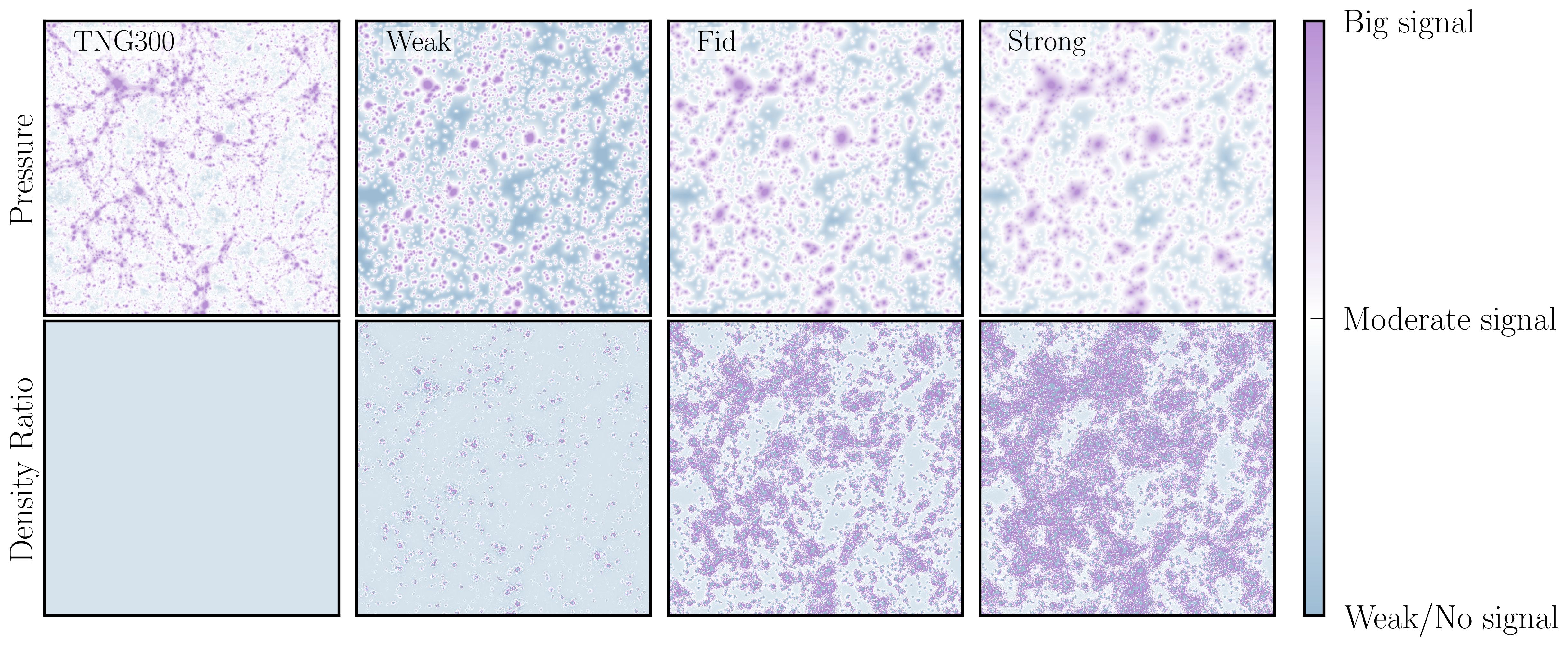
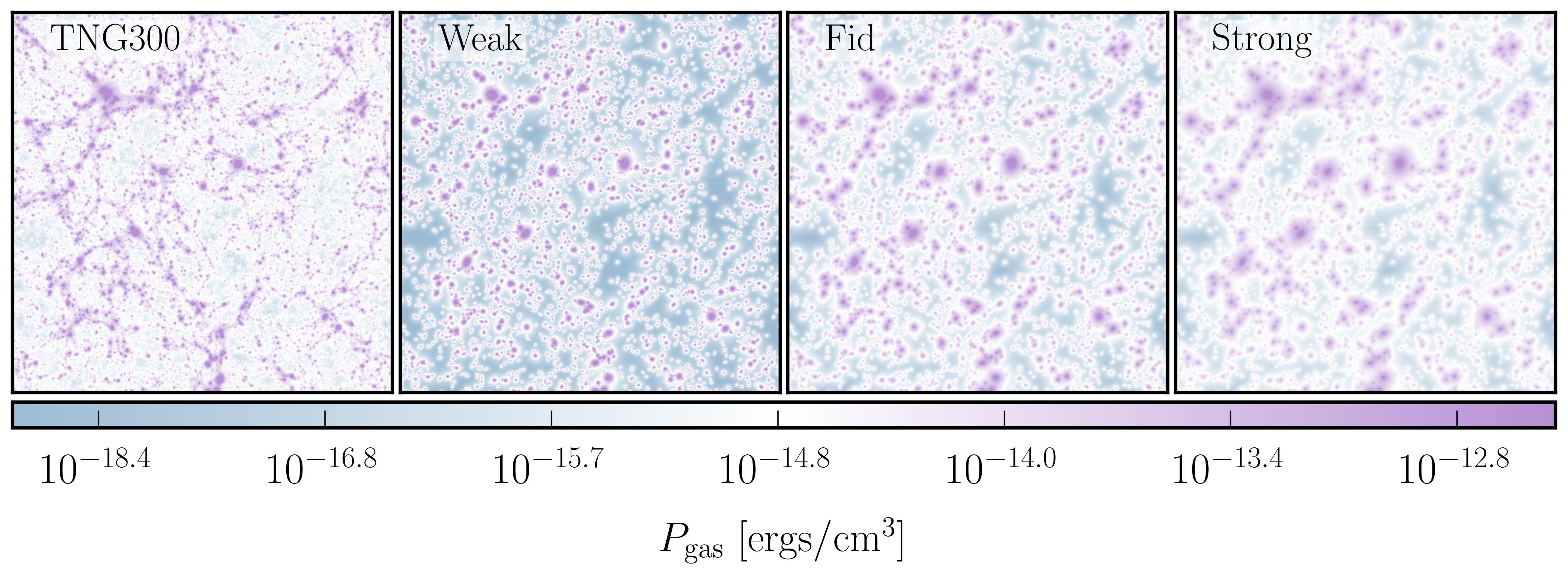
Example of how different baryonification models consistent impact the pressure (top) and density (bottom). We normalize the bottom row by the TNG density field (hence why the left panel is constant). Locations with high pressures are also accompanies by larger distortions in the density field. BaryonForge provides a consistent, connected model of the two.
Halo-model predictions from BCEmu, Bacco, and HMx
BaryonForge is highly modular, and so it is easy to implement additional models. In R.S, Pandey, Anbajagane, Krause+ 2025 we tested these models against the Magneticum simulations. In particular, we did a deep dive into the flexibility within each model and how easily the models could be fit to a set of observes “X” and predict a different set “Y”.
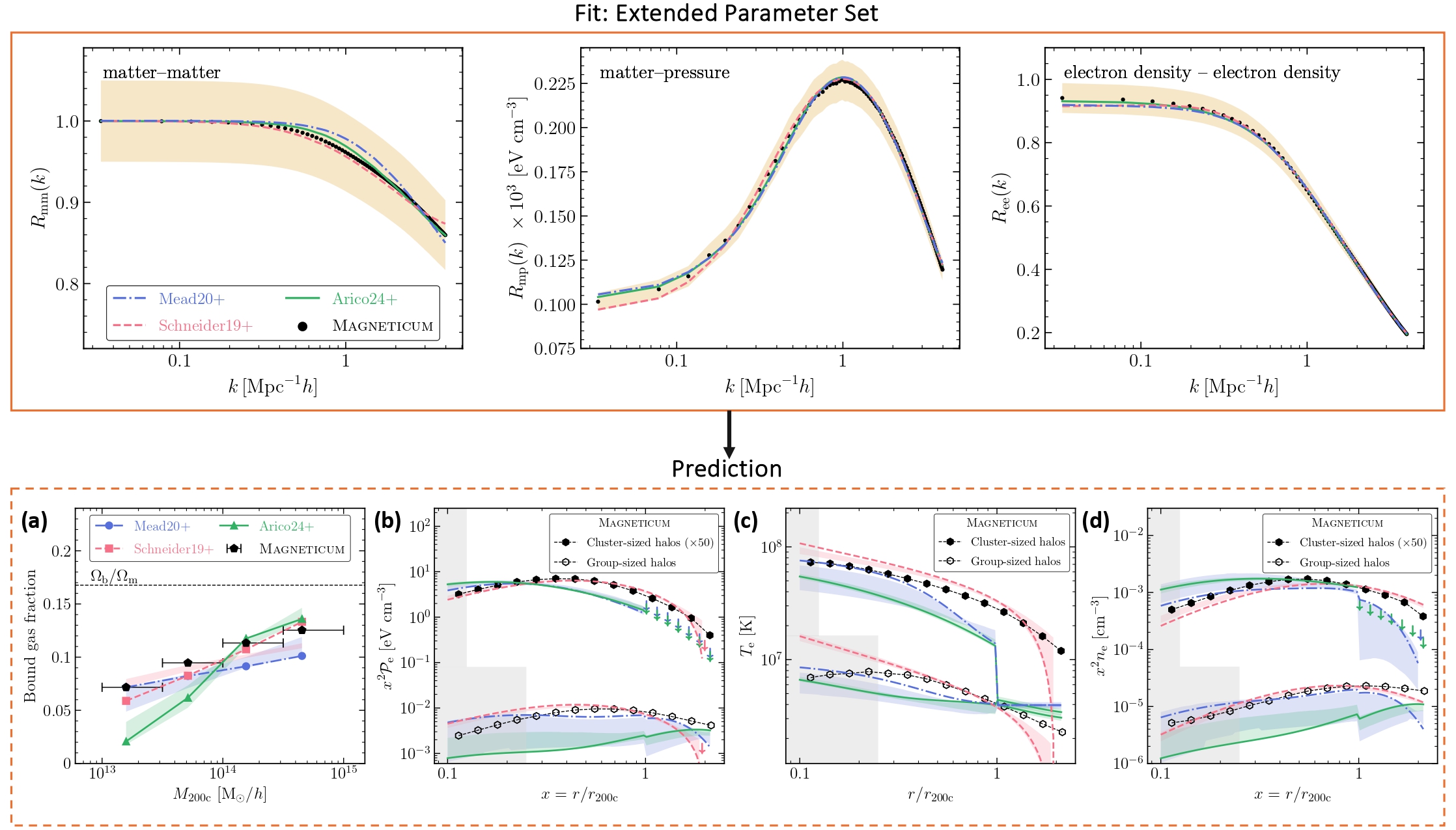
Figure 7 in R.S+ 2025. The halo-model based predictions are fit to a set of three power spectra and can predict the matter fractions and halo profiles in a consistent manner. The Schneider model performs the best, while the other two are still reasonable though not quite as precise.
